Ⅰ. 基础模型

A. 01背包

即每个物品要么选，要么不选。我们可以设状态 $f_{i,j}$ 表示考虑前 $i$ 个物品总体积 $\leq j$ 的最大价值，于是状态转移如下：

$$
f_{i,j}=\max(f_{i-1,j},f_{i-1,j-w_i}+v_i)
$$

前一个表示不选第 $i$ 个物品的情况，后一个表示选第 $i$ 个物品的情况。

初始化：$f_{i,j}=0$ 。

考虑怎么统计方案数。状态定义一样，但是表示的是方案数，于是又有转移方程如下：

$$
f_{i,j}=f_{i-1,j}+f_{i-1,j-w_i}
$$

初始化：$f_{i,0}=f_{0,j}=1$ 。

考虑优化空间，我们发现，每次转移只会用到上一维的状态，于是就可以把DP数组压成一维。代码如下：

1
2
3
4
5

for (int i = 1; i <= n; i++) {
	for (int j = m; j >= w[i]; j--) {
		f[j] = max(f[j], f[j-w[i]]+v[i]);
	}
}

B. 完全背包

就是在01背包的基础上每个物品可以选任意多个。状态设计同01背包，转移如下：

$$
f_{i,j}=\max(f_{i-1,j},f_{i,j-w_i}+v_i)
$$

区别在哪里呢？完全背包可以从当前的 $i$ 的状态转移过来，因为一个物品可以一选再选。

初始化、变形成方案数统计和压空间和上面的01背包大同小异，不过多赘述。贴个优化空间代码：

1
2
3
4
5

for (int i = 1; i <= n; i++) {
	for (int j = w[i]; j <= m; j++) {
		f[j] = max(f[j], f[j-w[i]]+v[i]);
	}
}

C. 多重背包

考试总结

Task 1

正解

性质题，找规律。

规律如下：

从 $n=15$ 开始：
$108,188,200,208,288,688,888,1088,1888,2008,2888,8888\dots$

容易发现 $a_n=a_{n-7}\times10+8\quad(n \geq 22)$

前14个要特判。

代码

1

无

关键点

暴力找规律。

死因

20 开头的规律没找到，就是没打暴力找规律。

Task 2

正解

搜索。

优化

这道题可以用 十字链表（Dancing Links X） 加速，但是爆搜就能跑出 $400\text{ms}$ 的好成绩。

别名：双向循环十字链表。

为什么能跑这么快

关键点：

• 对于这种搜索时间最不利的是 $5 \times 6$ 的矩阵，并且是无解的情况。
• 正常来说，如果不要求不能重复走点，时间复杂度最坏为 $O(2^{4} \times 3^{14} \times 4^{16})$ ，即四个角（4个）上的点有两种走法，边上的点（14个）有三种走法，内部的点（16个）有四种走法。
• 但是不能重复走点的情况下，时间复杂度最坏为 $O(1^{4} \times 2^{14} \times 3^{16})$，但是考虑到实际情况，加一个可行性剪枝，最后 $\text{dfs()}$ 函数大概只会运行到 $5 \times 10^6$ 次。
• 爆搜敢冲就能过。

题目来源

《永远的七日之都》

代码

1

无

死因

1

for (int i = 0; i <= n; i++)  // wssb

Task 3

正解

以 $dp$ 为辅助的搜索题。

说真的，这道题不难。一切的思路都是自然而然的，从爆搜到可行性剪枝再到用 $dp$ 完成可行性剪枝，最后实现的代码难度也不高。

关键点

$dp$ 可能不是一道题的全部而是一道题的部分。

思路

• 先想爆搜，同一位按字典序从大到小搜，期望得分：$30-40;pts$。
• 再想剪枝，用 $dp$ 判定后面有没有可能有解，计算一个点后最多能获取到的权值，再加上已经搜到的权值看它能不能 $\geq x$ 。
• 怎么做 $dp$ ？记录 $dp$ 长度和最后一位，预处理 $dp$ 时间复杂度为 $O(4n)$ 。整个算法时间复杂度见课后思考。

课后思考

• 整体时间复杂度是 $O(n+k)$ 还是 $O(nk)$ ？理论分析应该是 $O(n+k)$ 。

代码

1

无

死因

并没有死，打了暴力。还是全场唯一得分点（$30;pts$）。

但是事实上我的暴力打得还有优化空间且有一个小问题。

Task 4

正解

区间 $dp$ 。

思路

• 考虑朴素区间 $dp$ ，对于每个 $l\sim r$ 区间，枚举小区间并转移，时间复杂度 $O(n^4)$ 。
• 但是这种做法会 $\text{WA}$ 掉，因为这样记录状态会有情况没考虑到。所以考虑重设状态 $f_{i,j,max,min}$ 表示区间 $i\sim j$ 内已经通过多次操作后剩下的最大值为 $max$ 、最小值为 $min$ 时，所花的最小代价。而后我们定义 $ans_{i,j}$ 为 $i\sim j$ 这段区间被选空的最终答案（就是题目中说的那个最后输出的答案）。
• 接下来考虑怎么转移。$ans_{i,j}$ 的转移很简单，就是 $ans_{i,j}=max(f_{i,j,max,min}+a+b\times(max-min))$ 。而 $f_{i,j,max,min}$ 的转移，首先应该枚举中间断点 $k$ 就应该有以下三种情况：
  • $min$ 与 $max$ 都在左边，右边被选空：$f_{i,j,max,min}=f_{i,k,max,min}+ans_{k+1,j}$ 。
  • $min$ 与 $max$ 都在右边，左边被选空：$f_{i,j,max,min}=ans_{i,k}+f_{k+1,j,max,min}$ 。
  • $min$ 与 $max$ 左右两边都有：$f_{i,j,max,min}=f_{i,k,max,min}+f_{k+1,j,max,min}$ 。
• 容易发现的是，这样转移肯定不会少考虑情况，接下来就是考虑这么转移是否会多考虑情况？如果多考虑了，对答案有没有影响？
• 【这里不会】（zhw看到了comment一下）
• 结论：会多考虑情况但是这些情况不会比答案更优。
• 注意点：$w_i \leq 1000$ ，需要离散化处理。

来源

THUSC 2016 成绩单

代码

1

无

区间DP总结

• 区间DP是变化之神！
• $\text{Link Start!}$

通过例题看看区间DP的一些套路和新的思路。

不如按题目分类来说。

A~E 普通/模板区间DP

• 能量项链——普通区间DP
• 石子合并（加强版）——四边形不等式优化（不要求掌握）
• 【USACO 3.3.5】A Game游戏 IOI’96——带了博弈论的区间DP（个人觉得有点意思）
• 做错的作业——括号匹配类型的区间DP
• 【CQOI 2007】涂色——涂色类型区间DP

F,G 凸多边形区间DP

这一类型的DP特点是建立模型比较难。

要点梳理：

• 无论从哪一个点开始都一样，因此不必拆环成链。
• 状态定义为：$f_{i,j}$ 表示将 $i\sim j$ 这一段点的区间转化为三角形的最小价值。
• 状态转移为：$f_{i,j}=\min(f_{i,j},f_{i,k}+f_{k,j}+\text{cost}(i,j,k))$ ，即 $k$ 是两个子区间的公共端点， 而将他们合并后能组合出新的三角形 $\Delta A_iA_jA_k$ ，因此要加上这个新三角形造成的权值。

H 字符串折叠

我认为这道题的思路是捋得最清的，因为这道题真的很简单。

大致思路就是有两种转移：一是组合两段已压缩的区间，二是将这段区间压缩，时间复杂度大致为 $O(n^4)$ ，能刚刚好卡着过（据说用预处理或哈希或KMP找最长重复子串的长度能够将这道题卡到 $O(n^3)$ 的时间复杂度，然鹅我不会）。

R 压缩

这也是一道压缩字符串的题目。

但是这里对 $M$ 和 $R$ 的处理要更为复杂。

具体而言，这道题的 $f_{i,j,k}\quad(1\leq i\leq j\leq n,k\subset{0,1})$ 多了一维，用于标记 $i\sim j$ 这段区间内是（$1$）否（$0$）存在 $M$ 。

状态转移：

• $f_{i,j,0}=f_{i,k,0}+j-k$
• $f_{i,j,1}=\min(f_{i,k,0},f_{i,k,1})+\min(f_{k+1,j,0},f_{k+1,j,1})$
• $f_{i,j,0}=f_{i,mid,0}+1\quad\text{when }[i,j]\text{ can compress}$

J 表达式的亿种可能性

最有意义的题目之一。

维护的 $f_{i,j}$ 就是答案所求，关键就在转移。

弄清楚以下几点：

• $\times$ 的转移不需要别的东西，只需要 $f_{i,j}=f_{i,k}\times f_{k+1,j} \times\text{val}$
• $+$ 和 $-$ 的转移需要考虑左边的括号个数和右边的括号个数（详见第一次提交内的代码推导），最终转移式为：$f_{i,j}=((j-k-1)!f_{i,k}+(k-i)!f_{k+1,j})\times\text{val}$
• 但是以上转移式只考虑了先放完左边的括号再放右边的括号，然而，我们可以左右交替来回放，并且，左边内括号的顺序已经是我们在 $f_{i,k}$ 中内定好的了。因此 $\text{val}=\frac{(j-i-1)!}{(k-i)!(j-k-1)!}$ 作为系数。

M 有味道的数字

最具有启发性的一题。

这道题有几个性质需要搜索搜出来——只有 $3$ 和 $7$ 无法表示，表示 $5000$ 以内的数字最多只会用到长度为 $11$ 的前缀。

$f_{i,j}$ 表示 $i\sim j$ 这段区间内能表示出来的值（是个数组）这种思想有个很NB的名字叫做 **离散_____**（人话：打表）。

即用 $\text{vector}$ 存储值，单次转移时间复杂度就是 $O(nm)$ （ $n,m$ 表示合并的两个 $\text{vector}$ ） ，玄学下降！

而转移嘛……人人都会。

Q 单调栈

搜索最上牌面的一题。

这道题思路没什么好说的，只是注意一下有的时候记忆化搜索比循环区间DP好写。

区间DP的一点小知识

我个人一般会这么打区间DP：

1
2
3
4
5
6

for (int len = 2; len <= n; len++) {
	for (int i = 1; i+len-1 <= n; i++) {
		int j = i+len-1;
		// ...
	}
}

然而这么打常数是比较大的，优化写法：

1
2
3
4
5

for (int j = 2; j <= n; j++) {
	for (int i = j-1; i >= 1; i--) {
		// ...
	}
}

据说这样能优化很多。

我认为区间DP还有一类很重要的题，典型例题：关路灯

区间DP的特征

• 在操作中需要将两端区间合并，合并时存在固定的转移关系。
• 在操作中需要将子区间转移。

怎么看需不需要多开维数

很明显，当目前的状态定义会出现明显重复统计或是限制条件不够时要多开空间。

〇. 前置知识

• 四边形不等式（几何意义上）

  对于任意一个凸四边形（如图1），四个顶点分别为 $A,B,C,D$ ，其对角线交于点 $O$ ，则有 $AD+BC>AB+CD$ 以及 $AD+BC>AC+BD$ .

  证明：

  $\because AO+BO>AB\text{ and }CO+DO>CD$ （三角形两边长之和大于第三边）

  $\therefore (AO+DO)+(BO+CO)>AB+CD$ （联立两不等式）

  $\therefore AD+BC>AB+CD$

  （同理可得 $AD+BC>AC+BD$）

• 四边形不等式（DP意义上）

  这边主要都是些定义，因此不会有什么 针对定义的证明 。

  • 定义1

    设 $w$ 是定义在整数集合上的二元函数，对于任意整数 $i \leq i’ \leq j \leq j’$ ，若有 $w(i,j)+w(i’,j’) \leq w(i,j’)+w(i’,j)$ ，则称 $w$ 满足四边形不等式.[^1]

    什么叫做定义在“整数集合上的二元函数”？就是 $w$ 函数有两个参数，它的值和参数均为整数.

    但是，这似乎跟四边形没有半点关系吧.我们不如形象一点，对于刚才的定义，我们将 $i,i’,j,j’$ 表示在一个不太严谨的数轴上，这个数轴上 $a,b$ 两点的距离是 $w(a,b)$，然后，将中间的两个点，也就是 $i’$ 和 $j$ 向上抬升一点（如图2），这个四边形（在 $i’=j$ 的情况下是三角形）就出来了.

    

  • 定义2

    这是 定义1 的特殊情况。

    对于任意整数 $i < i+1 \leq j < j+1$ ，若有 $w(i,j)+w(i+1,j+1) \leq w(i,j+1)+w(i+1,j)$ ，则称 $w$ 满足四边形不等式.[^1]

    没啥好说的。。。

  • 单调性

    设 $w$ 是定义在整数集合上的二元函数，对于任意整数 $i \leq i’ \leq j \leq j’$ ，若有 $w(i,j’) \geq w(i’,j)$ ，则称 $w$ 具有单调性.[^1]

一. 证明四边形不等式定理

• 四边形不等式定理

  如果 $w(i,j)$ 满足四边形不等式和单调性，则使用动态规划计算 $f$ 数组的时间复杂度为 $\Theta(n^2)$ .

  • 引理1

• 1

二. 引用

[^1]: 参考 罗勇军的博客——算法竞赛专题解析（10）：DP优化(1)–四边形不等式

[^2]:F. Frances Yao原论文

动态规划（Dynamic programming）是一种神奇的喵。

动态规划的基本性质以及几个重要概念

忘记过去的人，必定要重蹈覆辙。 ——乔治·桑塔亚纳

几个性质

• 最优子结构
  这个特性也会在贪心算法中出现。

• 无后效性
  已经求解的子问题，不会再受到后续决策的影响。

• 子问题重叠
  见上文引用。

几个重要概念

• 状态
  即 dp 数组中每个位置的含义。

• 状态转移方程
  单纯讨论 dp 数组中的状态的转移关系，这一步将会非常关键。

• 初始状态定义
  也就是一开始的时候，哪些状态的值是可以直接确定的并且在状态的转移中无法被计算甚至会影响状态转移的。（我有很多次都是因为 dp 初始值导致来回调代码）

接下来我们会用一道题目来看一下这些定义是什么。

简单例题

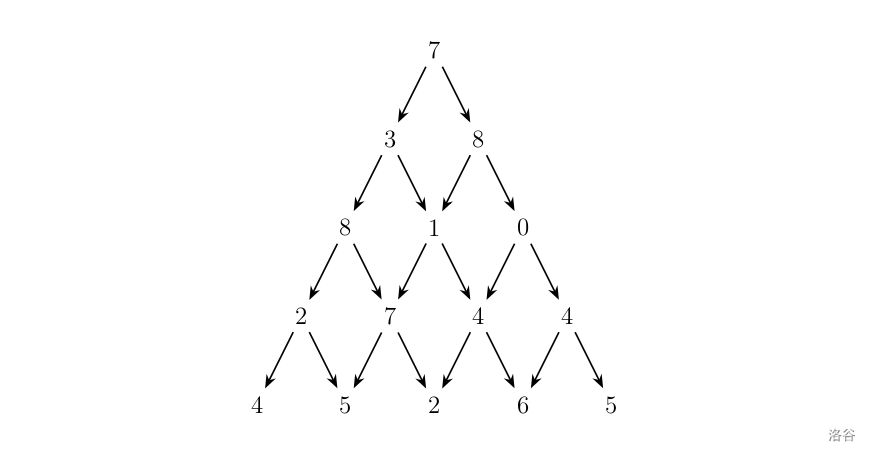
IOI1994 数字三角形
简单来说，给定一个由数组成的三角形（即除第一层只有一个数外，每一层的数个数都比上一层多1），需要你求出从第一层到最后一层的所经过的最大的和。

例如这个三角形，从 $7→3→8→7→5$ 的路径产生了最大权值。

这道题很简单，所以只在此处明确一下以上的概念。
下文中的 dp 数组未经优化，是二维数组，并且思路是从上往下进行计算。

状态：dp[i][j] 表示从上往下走到第 i 行第 j 列所能得到的最大权值。

状态转移方程：dp[i][j] = max(dp[i-1][j], dp[i-1][j-1]) + a[i][j]

初始状态定义：dp[1][1] = a[1][1]（但其实定不定义无所谓的啦）

喵你已经掌握了这些基本概念了，接下来我们会各种形态的DP进行深入剖析喵

各种动态规划的形态

线性DP

这一种DP构造最简单，代表性问题是LIS(最长上升子序列)和LCS(最长公共子序列)。(因为连续序列太简单，所以不在此处讨论)

最长公共子序列(LCS)

我们定义 f[i][j] 为第一个数组 i 之前与第二个数组 j 之前的数能构成的最长公共子序列的长度。于是，稍加推导，可以得出状态转移方程：

$f_{i,j}=\begin{cases}f_{i-1,j-1}+1&\mathrm{if}\;s[i]=t[j]\\max(f_{i-1,j},f_{i,j-1})&\mathrm{otherwise.}\end{cases}$

（这应该看得懂吧。。。）

接下来考虑初始状态，很明显，根本不需要定义初始状态。

接下来就是考验码力的时候了（好像也不怎么考验？

P.S. 如何提升码力？多做模拟题，尤其是大模拟，成为码力小王子！（我都没做

* So, end?

* Yeah, it’s easy. Isn’t it?

最长上升子序列(LIS)

请注意，LIS题目中还有很多类型的，例如求方案数或是判断一个数是否一定属于它所在的数组的LIS中。

我们定义 f[i] 表示前 i 个元素的最长上升子序列的长度。更新时，使用前面的所有合法状态来更新当前状态，容易写出转移方程：

$ f_{i}=\mathrm{max}(f_{j}\;|\;j<i\;\mathrm{and}\;A_j<A_i) $

这种方法的时间复杂度是 $O(n^2)$ ，并且我们还有第二种方法，它的时间复杂度是 $O(n\log n)$ 的。

首先我们定义一个数组 $d$ ，表示最长上升子序列，$len$ 为这个最长上升子序列的长度，所以 $d_{len}$ 就是这个最长上升子序列的最后一个元素。

我们初始化状态：$d_1=a_1, len=1$

接下来我们枚举 $i$ 从 $2$ 到 $n$ 每次更新 $d$ 数组。考虑接下来添加一个元素 $a_i$：

• 如果这个元素 $a_i \geq d_{len}$ ，就直接向最后添加一个元素。

• 否则我们在数组 $d$ 中找到第一个大于 $a_i$ 的元素与 $a_i$ 作替换。

完成！

背包问题

事实上在这个子问题下还有很多类问题，但是这类问题很简单，也肯定有人比我写得好，就不在此处说明了。

记忆化搜索

很难说它属于DP，但是它的思想却是实打实的DP。我们可以把这个词分为两块来理解：记忆化+搜索。还记得 Part 1 引用的那句话吗，记忆化搜索就是为了防止搜索时出现重复状态增加运行时间而出现的。具体而言，它在搜索过程中记录了每一步得到的答案，而下次这个同样的情况被搜索到时，将不会继续搜索，而是会把之前记录的答案直接返回。

这类问题有很多，包括后文中提到的 数位DP 的例题也是使用了记忆化搜索的。

解题步骤

1. 先看这道题能不能用记忆化搜索（这要保证搜索时产生的状态并不多）。

2. 如果可以，那么应该如何定义状态，需要记录的到底有什么（例如搜索时产生的步数信息就 一般 不用记录）。

3. 我下次复用这个信息的时候要注意什么。

区间DP

这类题目算是 玩的挺花 的题，各种变形出其不意攻其不备，并且状态的定义会比其他类型的题目灵活许多，因此对于这些题，最好的方法不是记模型，而是理解这种思路。因此，这个板块我们需要结合例题来看。

最经典的区间DP例题——石子合并（弱化版）

一条路上有许多堆石子，每堆石子都有一个质量参数，现在要将它们合并成一堆，每次合并的代价是这两堆石子的质量之和，需要求出合并成一堆的总代价的最小值。

题意很简单，现在我们来考虑状态的定义：$f_{i,j}$ 表示合并第 $i$ 到第 $j$ 堆石子所花费的代价的最小值。

接下来我们考虑转移：从 $i$ 到 $j$ 的石子可以把它分成两半来考虑，每次转移只需要增加两边的代价，也就是 $f_{i,j}=\mathrm{min}(f_{i,k}+f_{k+1,j}\;|\;i \leq k\leq j-1)$ （注意这个 $-1$ 哈）

那么，问题来了，$f$ 想要转移，前提是那些转移来的值是已经被处理过的，否则转了跟转了一样（sssss），所以，我们需要一种枚举方法，来保证转移的合法性。

这里你可以参考 floyd 的转移方法（事实上有人说 floyd 也是DP），我们只需要先枚举区间长度，再枚举起点，最后用前两个信息推出区间终点，我们考虑一下为什么这么做可以满足上面的性质，因为我们每次转移来的两个区间的长度一定是比当前区间的长度短的，而我们的区间长度又是从小到大枚举，自然而然转移来的状态一定是已经处理过的了。

另外，我们每次加的代价值，不能 再拿一个循环来枚举并累加代价，这里我们需要预处理一个前缀和以便我们在 $O(1)$ 的时间内的到代价值。

最后是初始状态，$f$ 数组首先肯定要赋值成极大值（这里注意，不建议将其赋值成 INT_MAX 或 LLONG_MAX ，这样 $f$ 数组一加就直接爆 int 或 long long，虽然这道题可以这么赋值），然后对于对角线上的元素 $f_{i,i}$ 要赋值成 $0$ 。

思考过程结束，代码如下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

#include <iostream>
#include <climits>
using namespace std;

int n, a[301];
int dp[301][301];
int c[301];

int main() {
    cin >> n;
    for (int i = 0; i <= n; i++) {
        for (int j = 0; j <= n; j++) {
            dp[i][j] = INT_MAX;
        }
    }
    for (int i = 1; i <= n; i++) {
        dp[i][i] = 0;
    }
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        c[i] = c[i - 1] + a[i];
    }
    for (int len = 2; len <= n; len++) {
        for (int i = 1; i <= n; i++) {
            int j = i + len - 1;
            if (j <= n) {
                for (int k = i; k < j; k++) {
                    dp[i][j] =
                        min(dp[i][j], dp[i][k] + dp[k + 1][j] + c[j] - c[i - 1]);
                }
            }
        }
    }
    cout << dp[1][n];
}

这道题事实上可以使用四边形不等式优化。但是我也忘了qwq。