2023-07-19发表2024-01-09更新学习总结 / 数学6 分钟读完 (大约901个字)

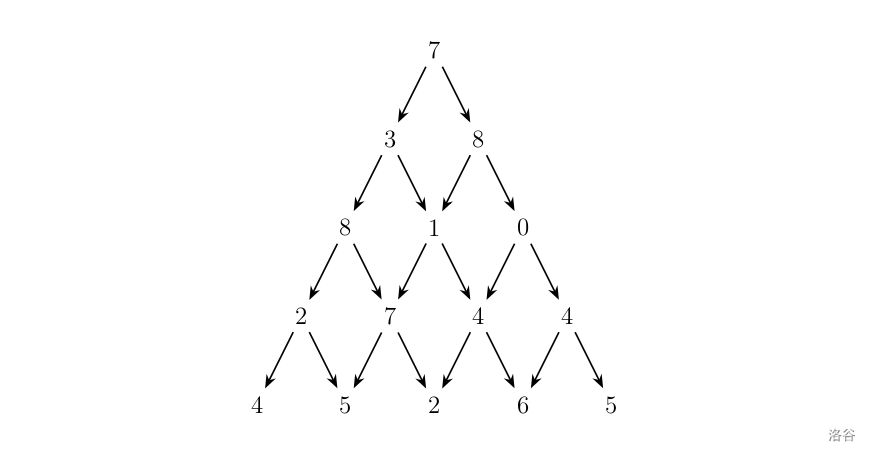
组合数

众所周知，组合数有两种求法。

杨辉三角求法：$\dbinom{i}{j}=\dbinom{i-1}{j}+\dbinom{i-1}{j-1}$
定义法：$\dbinom{i}{j}=\Large\frac{n!}{m!(n-m)!}$

其中，杨辉三角的空间占用很大，所以除非数据量较小（如：$N\leqslant 10^{4}$）的情况，我们不会使用这种求法，但是这种求法可以实现 $O(1)$ 查询，因此它也适用于需要大量查询的题目。而定义法适用于不需要大量查询（至少没有杨辉三角的情况多）的题目，但是因为有阶乘的存在，使得实现 $O(1)$ 还需要一点点数学上的优化，并且，其适用的数据范围（$N\leqslant 10^5$）一般都需要 $\text{mod}$ 一个极大数（阶乘不 $\text{mod}$ 留着爆 $\text{long long}$ 吗），然而我们都知道，同余的性质不适用于除法，这导致我们处于一个进退两难的地步。
古语有云：$\text{To modulo or not to do, it’s a question.}$
这时候，我们就需要乘法逆元来帮忙了。

乘法逆元

按照惯例，先说定义：如果一个线性同余方程 $ax\equiv 1(\mathrm{mod}\;b)$ ，则称 $x$ 为 $a\;\mathrm{mod}\;b$ 的逆元，记为 $a^{-1}$ 。我们可以把它理解成倒数，一种在模 $p$ 意义下的倒数。因此，我们可以知道一个数逆元的逆元就是这个数本身。
逆元的求法有两种：

`Extend-GCD` 拓展欧几里得法

就是直接解上述定义中的方程，没什么好说的。

void exgcd(int a, int b, int &x, int &y) {
	if (b == 0) {
		x = 1, y = 0;
		return ;
	}
	exgcd(b, a%b, x, y);
	y -= a/b*x;
	return ;
}

快速幂法

$\huge 使用这玩意的前提是\;b\;为质数！$

证明：

$\because ax\equiv 1(\mathrm{mod}\;b)$
由费马小定理: $a^{p-1}\equiv1(\mathrm{mod}\;b)$
得 $ax\equiv a^{p-1}(\mathrm{mod}\;b)$
$\therefore x\equiv a^{p-2}(\mathrm{mod}\;b)$

所以我们可以直接写一个快速幂板板！

int power(int a, int b) {
	b -= 2;
	int ans = 1;
	while (b) {
		if (b&1) ans = ans*a%p;
		a = a*a%p;
		b >>= 1;
	}
	return ans;
}

除此之外，我们还可以使用线性递推求一大串数的逆元（但是我不会推）。

$i^{-1}\equiv\begin{cases}1&\mathrm{if}\;i=1\-\left\lfloor\dfrac{p}{i}\right\rfloor (p\;\mathrm{mod}\;i)^{-1}&\mathrm{otherwise.}\end{cases}\;(\mathrm{mod}\;p)$

那么，归根结底，我们到底如何使用乘法逆元加速定义法的组合数呢？

乘法逆元优化组合数

我们不能使用定义法求带模组合数是因为除法不具备同余的性质，但是，我们可以用逆元将除法转化为乘法，进而求出组合数。
那么，原来的定义法公式可以转化为 $\dbinom{i}{j}=\large n!\times inv[m] \times inv[n-m]$（还是说可以把逆元理解为倒数）
首先，$n!$ 是可以预处理出来的，而 $inv[i]$ 使用上面说的两种方式很明显会 $TLE$ (但事实上并不会) ，剩下的只有一条路了——递推。
首先，我们还是可以使用上面说到的递推公式，但是对于阶乘，我们还有另一个递推公式：
$$inv[i!]=inv[(i+1)!]\times (i+1)$$
怎么理解呢？还记得我们说过，逆元就是一种倒数吗？借此，有如下公式：
$$ \frac{1}{i!}=\frac{1}{(i+1)!}\times (i+1) $$
答案已经呼之欲出了！

2023-07-18发表2024-01-09更新学习总结 / 动态规划11 分钟读完 (大约1638个字)

动态规划

动态规划（Dynamic programming）是一种神奇的喵。

动态规划的基本性质以及几个重要概念

忘记过去的人，必定要重蹈覆辙。 ——乔治·桑塔亚纳

几个性质

最优子结构
这个特性也会在贪心算法中出现。
无后效性
已经求解的子问题，不会再受到后续决策的影响。
子问题重叠
见上文引用。

几个重要概念

状态
即 dp 数组中每个位置的含义。
状态转移方程
单纯讨论 dp 数组中的状态的转移关系，这一步将会非常关键。
初始状态定义
也就是一开始的时候，哪些状态的值是可以直接确定的并且在状态的转移中无法被计算甚至会影响状态转移的。（我有很多次都是因为 dp 初始值导致来回调代码）

接下来我们会用一道题目来看一下这些定义是什么。

简单例题

IOI1994 数字三角形
简单来说，给定一个由数组成的三角形（即除第一层只有一个数外，每一层的数个数都比上一层多1），需要你求出从第一层到最后一层的所经过的最大的和。

例如这个三角形，从 $7→3→8→7→5$ 的路径产生了最大权值。

这道题很简单，所以只在此处明确一下以上的概念。
下文中的 dp 数组未经优化，是二维数组，并且思路是从上往下进行计算。

状态：dp[i][j] 表示从上往下走到第 i 行第 j 列所能得到的最大权值。

状态转移方程：dp[i][j] = max(dp[i-1][j], dp[i-1][j-1]) + a[i][j]

初始状态定义：dp[1][1] = a[1][1]（但其实定不定义无所谓的啦）

喵~~你已经掌握了这些基本概念了，接下来我们会各种形态的DP进行深入剖析喵~~

各种动态规划的形态

线性DP

这一种DP构造最简单，代表性问题是LIS(最长上升子序列)和LCS(最长公共子序列)。(因为连续序列太简单，所以不在此处讨论)

最长公共子序列(LCS)

我们定义 f[i][j] 为第一个数组 i 之前与第二个数组 j 之前的数能构成的最长公共子序列的长度。于是，稍加推导，可以得出状态转移方程：

$f_{i,j}=\begin{cases}f_{i-1,j-1}+1&\mathrm{if}\;s[i]=t[j]\\max(f_{i-1,j},f_{i,j-1})&\mathrm{otherwise.}\end{cases}$

（这应该看得懂吧。。。）

接下来考虑初始状态，很明显，根本不需要定义初始状态。

接下来就是考验码力的时候了~~（好像也不怎么考验？~~

P.S. 如何提升码力？多做模拟题，尤其是大模拟，成为码力小王子！~~（我都没做~~

* So, end?

* Yeah, it’s easy. Isn’t it?

最长上升子序列(LIS)

请注意，LIS题目中还有很多类型的，例如求方案数或是判断一个数是否一定属于它所在的数组的LIS中。

我们定义 f[i] 表示前 i 个元素的最长上升子序列的长度。更新时，使用前面的所有合法状态来更新当前状态，容易写出转移方程：

$ f_{i}=\mathrm{max}(f_{j}\;|\;j<i\;\mathrm{and}\;A_j<A_i) $

这种方法的时间复杂度是 $O(n^2)$ ，并且我们还有第二种方法，它的时间复杂度是 $O(n\log n)$ 的。

首先我们定义一个数组 $d$ ，表示最长上升子序列，$len$ 为这个最长上升子序列的长度，所以 $d_{len}$ 就是这个最长上升子序列的最后一个元素。

我们初始化状态：$d_1=a_1, len=1$

接下来我们枚举 $i$ 从 $2$ 到 $n$ 每次更新 $d$ 数组。考虑接下来添加一个元素 $a_i$：

如果这个元素 $a_i \geq d_{len}$ ，就直接向最后添加一个元素。
否则我们在数组 $d$ 中找到第一个大于 $a_i$ 的元素与 $a_i$ 作替换。

完成！

背包问题

事实上在这个子问题下还有很多类问题，但是这类问题很简单，也肯定有人比我写得好，就不在此处说明了。

记忆化搜索

很难说它属于DP，但是它的思想却是实打实的DP。我们可以把这个词分为两块来理解：记忆化+搜索。还记得 Part 1 引用的那句话吗，记忆化搜索就是为了防止搜索时出现重复状态增加运行时间而出现的。具体而言，它在搜索过程中记录了每一步得到的答案，而下次这个同样的情况被搜索到时，将不会继续搜索，而是会把之前记录的答案直接返回。

这类问题有很多，包括后文中提到的数位DP 的例题也是使用了记忆化搜索的。

解题步骤

先看这道题能不能用记忆化搜索（这要保证搜索时产生的状态并不多）。
如果可以，那么应该如何定义状态，需要记录的到底有什么（例如搜索时产生的步数信息就一般不用记录）。
我下次复用这个信息的时候要注意什么。

区间DP

这类题目算是 玩的挺花 的题，各种变形出其不意攻其不备，并且状态的定义会比其他类型的题目灵活许多，因此对于这些题，最好的方法不是记模型，而是理解这种思路。因此，这个板块我们需要结合例题来看。

最经典的区间DP例题——石子合并（弱化版）

一条路上有许多堆石子，每堆石子都有一个质量参数，现在要将它们合并成一堆，每次合并的代价是这两堆石子的质量之和，需要求出合并成一堆的总代价的最小值。

题意很简单，现在我们来考虑状态的定义：$f_{i,j}$ 表示合并第 $i$ 到第 $j$ 堆石子所花费的代价的最小值。

接下来我们考虑转移：从 $i$ 到 $j$ 的石子可以把它分成两半来考虑，每次转移只需要增加两边的代价，也就是 $f_{i,j}=\mathrm{min}(f_{i,k}+f_{k+1,j}\;|\;i \leq k\leq j-1)$ （注意这个 $-1$ 哈）

那么，问题来了，$f$ 想要转移，前提是那些转移来的值是已经被处理过的，否则转了跟转了一样（sssss），所以，我们需要一种枚举方法，来保证转移的合法性。

这里你可以参考 floyd 的转移方法（事实上有人说 floyd 也是DP），我们只需要先枚举区间长度，再枚举起点，最后用前两个信息推出区间终点，我们考虑一下为什么这么做可以满足上面的性质，因为我们每次转移来的两个区间的长度一定是比当前区间的长度短的，而我们的区间长度又是从小到大枚举，自然而然转移来的状态一定是已经处理过的了。

另外，我们每次加的代价值，不能再拿一个循环来枚举并累加代价，这里我们需要预处理一个前缀和以便我们在 $O(1)$ 的时间内的到代价值。

最后是初始状态，$f$ 数组首先肯定要赋值成极大值（这里注意，不建议将其赋值成 INT_MAX 或 LLONG_MAX ，这样 $f$ 数组一加就直接爆 int 或 long long，虽然这道题可以这么赋值），然后对于对角线上的元素 $f_{i,i}$ 要赋值成 $0$ 。

思考过程结束，代码如下。

#include <iostream>
#include <climits>
using namespace std;

int n, a[301];
int dp[301][301];
int c[301];

int main() {
    cin >> n;
    for (int i = 0; i <= n; i++) {
        for (int j = 0; j <= n; j++) {
            dp[i][j] = INT_MAX;
        }
    }
    for (int i = 1; i <= n; i++) {
        dp[i][i] = 0;
    }
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        c[i] = c[i - 1] + a[i];
    }
    for (int len = 2; len <= n; len++) {
        for (int i = 1; i <= n; i++) {
            int j = i + len - 1;
            if (j <= n) {
                for (int k = i; k < j; k++) {
                    dp[i][j] =
                        min(dp[i][j], dp[i][k] + dp[k + 1][j] + c[j] - c[i - 1]);
                }
            }
        }
    }
    cout << dp[1][n];
}

这道题事实上可以使用四边形不等式优化。但是我也忘了qwq。

2023-07-17发表2024-01-09更新学习总结 / 思想19 分钟读完 (大约2922个字)

分块与矩阵

update: 2023/12/12 fixed pictures

本文中所有图片均使用Power Point制作

分块部分

俗话说得好：

${ \Huge 暴力+暴力=分块 }$

分块总的来说就是线段树的阉割版，其时间复杂度基本维持在 $\sqrt N$ 数量级。一般的分块支持单点/区间查询以及单点/区间修改.

分块的块长一般是 $\sqrt N$ ( $N$ 是数组大小)，例如，对于一个数组 $A$ ，$|A| =13$ ，每一块的长度便是 $\sqrt {13}\approx3$ ，但是分块完成后我们会发现最后一块的大小是 $1$ ，不足其他块的大小(如下图).

分了块后我们便可以干很多事了，单点查询/修改就不说了，直接访问数组下标进行修改.我们来说说区间查询/修改，例如还是那个数组 $A$ ，现在我们要修改下标为 $2$ 到 $7$ 的区间，这个时候我们要对每一块生成一个懒标记，于是我们的思路便很明确了，对于这段区间里整块的部分直接修改懒标记，剩下的不足一整块暴力修改(如下图).同理，查询也是一样，只是要注意统计时要把所有懒标记加上，不管是整块还是不足整块.下面也会给出一份区间修改(增加)区间查询(最大值)的代码.

#include <bits/stdc++.h>
using namespace std;

const int inf = 0x3fffffff;
int n, m, s;
int a[100100], chunk[100100], lazy[100100];

void modify(int x, int y, int z) {
	int i = (x-1)/s+1;
	int j = (y-1)/s+1;
	chunk[i] = -inf;
	chunk[j] = -inf;
	if (i == j) {
		for (int k = x; k <= y; k++) {
			a[k] += z;
		}
		for (int k = (i-1)*s+1; k <= j*s; k++) {
			if (a[k] > chunk[i]) chunk[i] = a[k];
		}
	} else {
		for (int k = x; k <= i*s; k++) {
			a[k] += z;
		}
		for (int k = (i-1)*s+1; k <= i*s; k++) {
			if (a[k] > chunk[i]) chunk[i] = a[k];
		}
		for (int k = (j-1)*s+1; k <= y; k++) {
			a[k] += z;
		}
		for (int k = (j-1)*s+1; k <= j*s; k++) {
			if (a[k] > chunk[j]) chunk[j] = a[k];
		}
		for (int k = i+1; k < j; k++) {
			lazy[k] += z;
		}
	}
}

int search(int x, int y) {
	int i = (x-1)/s+1;
	int j = (y-1)/s+1;
	int ans = -inf;
	if (i == j) {
		for (int k = x; k <= y; k++) {
			if (a[k]+lazy[i] > ans) ans = a[k]+lazy[j];
		}
	} else {
		for (int k = x; k <= i*s; k++) {
			if (a[k]+lazy[i] > ans) ans = a[k]+lazy[i];
		}
		for (int k = (j-1)*s+1; k <= y; k++) {
			if (a[k]+lazy[j] > ans) ans = a[k]+lazy[j];
		}
		for (int k = i+1; k < j; k++) {
			if (chunk[k]+lazy[k] > ans) ans = chunk[k]+lazy[k];
		}
	}
	return ans;
}

signed main() {
	scanf("%d", &n);
	s = sqrt(n);
	for (int i = 1; i <= n; i++) {
		scanf("%d", a+i);
		if (i%s == 1 || a[i] > chunk[(i-1)/s+1]) chunk[(i-1)/s+1] = a[i];
	}
	cin >> m;
	while (m--) {
		char op[3];
		int x, y, z;
		scanf("%s%d%d", op, &x, &y);
		if (op[2] == 'D') {
			cin >> z;
			modify(x, y, z);
		} else {
			cout << search(x, y) << endl;
		}
	}
}

/*
Input:
5
1 2 3 2 5
5
ADD 1 4 3
ASK 2 3
ASK 3 5
ADD 2 4 2
ASK 2 5

Output:
6
6
8
*/

分块的大部分题目并不像这样简单，例如下面的动态区间第 $K$ 小数例题.

给定一个由 $N$ 个数组成的序列 ${A_1,A_2,…,A_N}$
每次可以将 $A_k$ 的值改为 $t$ ，或者提问序列中 ${A_l,..,A_r}$ 中第 $k$ 小的数的值.

对于这道题，我们需要使用另一个数组 $B$ 用来将每个块内的元素排序，需要查询时先使用二分答案，再在 check() 内对于整块的统计答案直接使用排序的数组进行二分，正所谓一个分块套二分再套二分，细节很多，详见下码.

void modify(int k, int t) {  // 单点修改，需要排序
	int F = (k-1)/s+1;
	a[k] = t;
	b[F].clear();
	for (int i = (F-1)*s+1; i <= F*s; i++) {
		b[F].push_back(a[i]);
	}
	sort(b[F].begin(), b[F].end());
}

int check(int x, int y, int f) {  // 统计信息
	int i = (x-1)/s+1;
	int j = (y-1)/s+1;
	int ans = 0;
	if (i == j) {
		for (int k = x; k <= y; k++) {
			if (a[k] < f) ans++;
		}
	} else {
		for (int k = x; k <= i*s; k++) {
			if (a[k] < f) ans++;
		}
		for (int k = (j-1)*s+1; k <= y; k++) {
			if (a[k] < f) ans++;
		}
		for (int k = i+1; k < j; k++) {
			ans += lower_bound(b[k].begin(), b[k].end(), f) -b[k].begin();  // 直接二分统计整块内的答案
		}
	}
	return ans;
}

int query(int x, int y, int k) {  // 二分答案
	int l = 0, r = 50005, mid;
	while (l+1 < r) {
		mid = (l+r)>>1;
		if (check(x, y, mid) >= k) r = mid;
		else l = mid;
	}
	return l;
}

除此之外，还有要同时开两个 lazy 的题目——数列分块入门7，关键在于处理两个运算法则之间的优先级.

数列分块入门5——在根号开到一定程度时块内的元素会全部变为 $1$，这时可以不用暴力统计，直接计算块长.

另外，还有一类分块题，算是属于半个块状数组(或者说块状链表).

众所周知，数组访问时间复杂度 $O(1)$ ，修改 $O(n)$ ，而链表访问 $O(n)$ ，修改 $O(1)$ .

而块状链表，就是两者的结合体，它查询 $O(\sqrt n)$ ，修改 $O(\sqrt n)$ ，两者时间复杂度相差不大，是个折中方案，具体长什么样见下图.

那我们应该如何维护来保证它们的时间复杂度呢？很简单，我们只需要在一个块的大小大于一定的值后暴力拆分成两块接在原块后面~~（什么细胞的无丝分裂~~，具体来说，我们要在一块的大小大于 $2\sqrt N$ 时分裂(注意：此处的 $N$ 指的是所有元素，包括了后面新增的元素，也就是说每次添加元素时要重新计算阈值长度).理清思路后，代码实现很简单了(见下，例题).

int cnt;  // 总块数，用于给新块编号
int nc;  // 元素总数

typedef pair<int, int> pii;  // 不会吧不会吧，都3202年了不会还有人不会用typedef吧

pii locate(int x) {  // 定位元素
	int i = 1;
	while (x > block[i].siz) {
		x -= block[i].siz;
		i = block[i].to;
	}
	return {i, x};
}
void split(int x, int y) {
	cnt++;
	for (int i = y; i <= block[x].siz; i++) {
		block[cnt].a[++block[cnt].siz] = block[x].a[i];
		block[x].a[i] = 0;
	}
	block[cnt].to = block[x].to;
	block[x].to = cnt;
}

// 临时定义一下（不要问我为什么不开变量
#define x p.first
#define y p.second
void insert(int t, int v) {
	pii p = locate(t);
    // 暴力插入
	for (int i = block[x].siz; i >= y; i--) {
		block[x].a[i+1] = block[x].a[i];
	}
	block[x].siz++;
	block[x].a[y] = v;
	nc++;
	s = sqrt(nc);
	if (block[x].siz >= 2*s) {
		split(x, block[x].siz/2+1);
		block[x].siz = block[x].siz/2;
	}
}
#undef x
#undef y

int query(int x) {  // 极简的查询的函数
	pii p = locate(x);
	return block[p.first].a[p.second];
}

除了一般的分块题和块状链表外，分块还有一个重要作用——莫队，它可以解决一部分的区间查询题目(尤其是查询某种区间有几种值的).

先说本质，本质并不是分块，而是双指针.莫队在运行时会用到两个数组，一个是原来的数组，另一个是 cnt 数组，cnt 数组是用来记录每个数出现的次数(在某些时候可能需要配合离散化食用).下面是算法基本的运行过程.

首先我们有两个指针 i 和 j ，先不考虑为什么他们在这个位置上，现在我们要把他们移到既定位置.我们有一种很简单的思路，先把左( i )移到既定位置的左端点，再把右( j )移到既定位置的右端点上.而在这个期间，我们可以顺便统计 cnt 数组，并且维护 tot 变量(统计种类，具体来讲是在 cnt 某个值从0到1或是从1到0的过程中修正).于是我们就有了一个基本的模型了，就是不断通过移动双指针来处理每个询问，但是很明显，这样移来移去，i 最多会移动 $MN$ 次( $M$ 是询问次数，$N$ 是数组长度)，j 也同理，这样的时间复杂度是不行的.而莫队算法就是在此处做了优化.

莫队首先会把询问离线，并把数组的点进行分块，而排序询问的第一关键字是每个询问左端点所在块的编号，而第二关键字是右端点.具体实现如下：

#include <bits/stdc++.h>
using namespace std;

int n, m, s;
int a[50050], cnt[1000010];
int ans[200020], tot = 0;  // ans是将答案还原的数组

struct node {
    int l, r, id;
} q[200020];

bool cmp(node a, node b) {
    if ((a.l-1)/s+1 == (b.l-1)/s+1) return a.r < b.r;  // 排序
    return a.l < b.l;
}

void add(int p) {
    if (++cnt[a[p]] == 1) tot++;  // 对应左端点左移与右端点右移
}

void del(int p) {
    if (--cnt[a[p]] == 0) tot--;  // 对应左端点右移与右端点左移
}

signed main() {
    cin >> n;
    s = sqrt(n);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    cin >> m;
    for (int i = 1; i <= m; i++) {
        cin >> q[i].l >> q[i].r;
        q[i].id = i;
    }
    sort(q+1, q+m+1, cmp);  // 处理询问
    int l = 0, r = 0;
    for (int i = 1; i <= m; i++) {
        while (r < q[i].r) add(++r);
        while (r > q[i].r) del(r--);
        while (l < q[i].l) del(l++);
        while (l > q[i].l) add(--l);
        ans[q[i].id] = tot;
    }
    for (int i = 1; i <= m; i++) {
        cout << ans[i] << endl;
    }
    return 0;
}

除此之外，莫队还有一种带修改版本.

不是说了将询问离线了吗，离线处理时怎么修改啊.

还是可以修改的，现在带修改功能得将修改的点还原到询问前的状态.

现在时间也得移来移去了.

嗯？时间移来移去？像 i 和 j 那样？

那这就好实现了啊.新增一维来处理时间.

具体怎么讲？

记录一下每次修改前后的状态，每次将时间移动时便一步步更换状态，直到回溯到指定时间，同时 cmp 函数也要改一下.

于是，我们就有了这个代码：

#include <bits/stdc++.h>
// 回避关键词检测的打包函数
#define pack1 {x, y, ccnt, qcnt}
#define pack2 {x, y}
using namespace std;

int l, r;
int n, m, s, tcnt;
int a[133344], cnt[1000010];
int ans[133344], tot;
int chunk[133344];

struct node{  // 记录询问
	int l, r, t, i;
}q[133344];
int qcnt;

bool cmp(node a, node b) {  // 新的排序函数
	if (chunk[a.l] == chunk[b.l] && chunk[a.r] == chunk[b.r]) return a.t < b.t;
	if (chunk[a.l] == chunk[b.l]) return a.r < b.r;
	return a.l < b.l;
}

struct cg{  // 记录修改
	int i, v;
}c[133344];
int ccnt;

void add(int p) {
	tot += !cnt[p]++;  // 用于l与r的修改，意义同上
}

void del(int p) {
	tot -= !--cnt[p];  // 同上
}

void timem(int i, int p) {
	if (q[i].l <= c[p].i && c[p].i <= q[i].r) {  // 时间更改器（雾
		del(a[c[p].i]);
		add(c[p].v);
	}
	swap(a[c[p].i], c[p].v);  // 因为有去必有回，所以下一次使用这个位置一定是把它更改回来
}

int main() {
	cin >> n >> m;
	s = pow(n*1.0, 2.0/3.0);  // 适用于莫队的特殊分块大小
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
		chunk[i] = (i-1)/s+1;  // 记录块号（也可以不记）
	}
	for (int i = 1; i <= m; i++) {
		char op;
		int x, y;
		cin >> op >> x >> y;
		if (op == 'Q') {
			q[++qcnt] = pack1;
		} else {
			c[++ccnt] = pack2;
		}
	}
	sort(q+1, q+qcnt+1, cmp);
	int l, r, t;
	l = r = t = 0;
	for (int i = 1; i <= qcnt; i++) {  // 将三个维度移至指定位置
		while (l < q[i].l) del(a[l++]);
		while (l > q[i].l) add(a[--l]);
		while (r < q[i].r) add(a[++r]);
		while (r > q[i].r) del(a[r--]);
		while (t < q[i].t) timem(i, ++t);
		while (t > q[i].t) timem(i, t--);
		ans[q[i].i] = tot;  // 记录答案
	}
	for (int i = 1; i <= qcnt; i++) {
		cout << ans[i] << endl;
	}
    return 0;
}

Part 分块思想 End

矩阵部分

咕一会…

update: 2023/12/12 还没写。。。

update: 2024/01/01 还没写。。。

2023-07-08发表2024-01-09更新学习总结 / 图论24 分钟读完 (大约3568个字)

二分图与图的连通

update: 2023/12/12 fixed pictures

学习内容

本周学习内容：

Week 1
|- 二分图
|  |- 二分图的判定
|  |  |- 染色法
|  |  |- 不存在奇环（长为奇数的环）
|  |- 二分图最大匹配（匈牙利算法）
|  |- 二分图最小点覆盖（König定理二分：二分图中，最小点覆盖=最大匹配）
|  |- 二分图最大独立集（二分图中，最大独立集=n-最小点覆盖）
|  |- 例题（关于建边）
|- 图的联通
|  |- 定义（只有概念，详细定义见下）
|  |  |- 无向图中的定义
|  |  |  |- 连通图
|  |  |  |- 子图
|  |  |  |- 连通子图
|  |  |  |- 连通分量（最大联通子图）
|  |  |- 有向图中的定义
|  |  |  |- 强连通图
|  |  |  |- 强连通子图
|  |  |  |- 强连通分量
|  |  |  |- k连通图（双连通图）
|  |  |  |- 割点
|  |  |  |- 桥
|  |  |  |- 双连通分量
|  |  |  |- 点双连通分量
|  |  |  |- 边双连通分量
|  |- 算法
|  |  |- 如何求强连通分量（SCC）= 如何缩点
|  |  |  |- Kosaraju算法
|  |  |  |- Tarjan算法
|  |  |  |- Gabow算法（略）
|  |  |- 如何求桥/割点
|  |  |  |- Tarjan算法（对还是它）
|  |  |- 如何求点/边双连通分量
|  |  |  |- Tarjan算法（啊？）

学习内容的模板（以及图论常用模板）

二分图最大匹配（König算法）

例题

vector<int> g[MAXN];
bool vis[MAXM];
int lst[MAXM];

bool konig(int u) {
	for (auto &v : g[u]) {  // auto好用的
		if (vis[v]) continue;
		vis[v] = 1;
		if (lst[v] == 0 || findargu(lst[v])) {
			lst[v] = u;
			return 1;
		}
	}
	return 0;
}

int main() {
    int cnt = 0;
	for (int i = 1; i <= n; i++) {
		memset(vis, 0, sizeof vis);  // 打时间戳可以优化常数
		if (findargu(i)) cnt++;
	}
	cout << cnt;
}

强连通分量（SCC）以及缩点

例题（附带最短路）

vector<int> g[MAXN];
int dfn[MAXN], low[MAXN], dfncnt;  // 两个关键数组：dfn, low
bool ins[MAXN];
int st[MAXN], top;  // 手写栈
int tag[MAXN], tagcnt;  // 标记数组，tagcnt是强连通分量的个数

void tarjan(int u) {
	dfn[u] = low[u] = ++dfncnt;
	ins[u] = 1;
	st[++top] = u;
	for (auto &v : g[u]) {
		if (!dfn[v]) {
			tarjan(v);
			low[u] = min(low[u], low[v]);
		} else if (ins[v]) low[u] = min(low[u], dfn[v]);
	}
	if (dfn[u] == low[u]) {
		tagcnt++;
		while (1) {
			int v = st[top--];
			ins[v] = 0;
			tag[v] = tagcnt;
			if (v == u) break;
		}
	}
}

int main() {
    // 因为不确定图是否连通，所以对于每一个点都要跑一遍Tarjan
    for (int i = 1; i <= n; i++) {
		if (!dfn[i]) tarjan(i);
	}

    // 缩点(建新图)
    vector<int> h[MAXN];
    for (int i = 1; i <= m; i++) {
        if (tag[e[i].u] != tag[e[i].v]) {
            h[tag[e[i].u]].push_back(tag[e[i].v]);
        }
    }
}

割点

例题

vector<int> g[MAXN];
int dfn[MAXN], low[MAXN], dfncnt;
int tag[MAXN], tagcnt;  // 求割点不需要使用栈

// 割点
bool cut[MAXN];  // 标记那些点是割点
int cnt;  // 统计割点个数
void tarjan(int u, int f) {
	dfn[u] = low[u] = ++dfncnt;
	int sons = 0;
	for (auto &v : g[u]) {
		if (!dfn[v]) {
			tarjan(v, u);
			sons++;
			low[u] = min(low[u], low[v]);
			if (low[v] >= dfn[u] && !cut[u] && u != rt) {  // 割点的判断-1
				cut[u] = 1;
				cnt++;
			}
		} else if (dfn[v] < dfn[u] && v != f) low[u] = min(low[u], dfn[v]);
	}
	if (u == rt && sons >= 2 && !cut[u]) {  // 割点的判断-2
		cut[u] = 1;
		cnt++;
	}
}

桥

~~例题（没有例题，不要点开）~~

vector<int> g[MAXN];
int dfn[MAXN], low[MAXN], dfncnt;
int tag[MAXN], tagcnt;  // 求桥还是不需要使用栈

// 桥（输出到stdout）
void tarjan(int u, int f) {
	dfn[u] = low[u] = ++dfncnt;
	int sons = 0;
	for (auto &v : g[u]) {
		if (!dfn[v]) {
			tarjan(v, u);
			sons++;
			low[u] = min(low[u], low[v]);
			if (low[v] > dfn[u]) {  // 桥的判断
				cout << u << " " << v << endl;
			}
		} else if (dfn[v] < dfn[u] && v != f) low[u] = min(low[u], dfn[v]);
	}
}

点双连通分量

例题

int dfn[MAXN], low[MAXN], dfncnt;
int tag[MAXN], tagcnt;
stack<int> st;
int rt;
vector<int> ans[MAXN];
int cnt;

void tarjan(int u) {
	dfn[u] = low[u] = ++dfncnt;
	st.push(u);
	if (u == rt && !head[u]) {  // 判断孤立点
		ans[++cnt].push_back(u);
		return ;
	}
	for (int i = head[u]; i; i = g[i].nxt) {  // 这里使用链式前向星
		int v = g[i].to;
		if (!dfn[v]) {
			tarjan(v);
			low[u] = min(low[u], low[v]);
			if (low[v] >= dfn[u]) {
				cnt++;
				int p;
				do {
					p = st.top();
					st.pop();
					ans[cnt].push_back(p);
				} while (v != p);
				ans[cnt].push_back(u);
			}
		} else low[u] = min(low[u], dfn[v]);
	}
}

dijkstra算法

例题0 例题1 例题2 （例题0是板子，例题1-2是缩点+最短路）

// 值得注意的一点是，dijkstra算法处理最长路时会损失效率（虽然可以卡过），所以在处理最长路时使用SPFA会更加有效（尽管它死了）
// 上述内容对应例题2，如果使用dijkstra算法的话会WA#3
struct node{
	int dis, u;
	bool operator < (const node& a) const {
		return dis > a.dis;
	}
};

bool vis[MAXN];
int dis[MAXN];
priority_queue<node> q;

void dijkstra(int s) {
	memset(dis, 0x3f, sizeof dis);
	dis[s] = 0;
	q.push({0, s});
	while (!q.empty()) {
		int u = q.top().u;
		q.pop();
		if (vis[u]) continue;
		vis[u] = 1;
		for (auto &i : h[u]) {
			int v = i.first, w = i.second;
			if (dis[v] > dis[u]+w) {
				dis[v] = dis[u]+w;
				q.push({dis[v], v});
			}
		}
	}
}

SPFA算法

例题0 例题1 （例题0是板子，例题1是缩点+最短路）

// SPFA尽管死了并且它的效率要比dijkstra慢，但是其拥有良好的负环检测系统，关键是：最长路能用
vector<int> h[500010];
int dis[500010], cnt[500010];
bool vis[500010];
queue<int> q;

// 这是最长路并且统计的是点权，改为最短路/统计边权只要参考dijhstra就好
bool spfa() {
	memset(dis, -1, sizeof dis);  // 最短路需改
	int f = tag[s];
	q.push(f);
	dis[f] = mon[f];
	vis[f] = 1;
	while (!q.empty()) {
		int u = q.front();
		q.pop();
		vis[u] = 0;
		for (auto &i : h[u]) {
			if (dis[i] < dis[u]+mon[i]) {  // 最短路/统计边权需改
				dis[i] = dis[u]+mon[i];  // 最短路/统计边权需改
				cnt[i] = cnt[u]+1;
				if (cnt[i] >= tagcnt) return 0;
				if (!vis[i]) {
					q.push(i);
					vis[i] = 1;
				}
			}
		}
	}
	return 1;
}

学习内容——各种定义

强连通/连通图

在无向图中，任意两点都直接或间接连通，则称该图为 连通图(connected).

相应的，有向图中任意一点都存在路径到达任意另一点，则称该有向图为 强连通图(strong connected) .

子图

在一个图 $H$ 中，$H$ 的所有边属于图 $G$ 的所有边，$H$ 的所有点属于图 $G$ 的所有点，则称图 $H$ 是图 $G$ 的 子图(subgraph) .

连通分量

无向图 $G$ 的最大连通子图称为 $G$ 的 连通分量(connected components) .

何为最大连通子图？这个子图是 $G$ 的连通子图，将 $G$ 的任何一个不在这张子图中的点加入这张子图后，该子图不再连通.

强连通分量（SCC）

在任意有向图中能够实现强连通的部分我们称其为 **强连通分量(Strongly connected component)**，如下图，蓝色框内的分别是一个强连通分量.

如果把每个强连通分量收缩为单个顶点，得到的是一个 **有向无环图(DAG)**，于是我们可以在这个图的基础上进行拓扑排序，详见此例题.

而求这个强连通分量，我们可以使用两个算法：Kosaraju算法，Tarjan算法.

Kosaraju算法的流程如下：

重复寻找图 $G$ 中未被讨论的点，从它开始DFS后序遍历图 $G$ ，遍历到的点置为已讨论，用数组记录每个点到达的先后次序，直到找不到没有讨论的点.
将图 $G$ 反向得到图 $G’$ ，重置所有点为未讨论.
一直从数组中未讨论的最后一个点出发，DFS后续遍历图 $G’$ ，DFS每完成一次，就说明找到了一个强连通分量，直到数组中没有未讨论的点.

这是Kosaraju算法的模板（之所以Kosaraju算法没有放在SCC的模板内，是因为这个算法相对于Tarjan算法少用很多）：

bool g[1001][1001];  // 这里使用的是邻接矩阵
bool vis[1001];
int lis[1001], cnt = 0;
int tag[1001], scc = 0;
bool ind[1001];

void dfs1(int u) {
	vis[u] = 1;
	for (int i = 1; i <= n; i++) {
		if (g[u][i] && !vis[i]) dfs1(i);
	}
	lis[++cnt] = u;
}

void dfs2(int u) {
	vis[u] = 1;
	tag[u] = scc;
	for (int i = 1; i <= n; i++) {
		if (g[i][u] && !vis[i]) dfs2(i);  // 这里注意，判断的边是g[i][u]，因为我们要在反图上跑dfs2()
	}
}

int main() {
	for (int i = 1; i <= n; i++) vis[i] = 0;  // 这里可以用memset
	for (int i = 1; i <= n; i++) {
		if (!vis[i]) dfs1(i);
	}
	for (int i = 1; i <= n; i++) vis[i] = 0;
	for (int i = cnt; i >= 1; i--) {
		if (!vis[lis[i]]) {
			scc++;
			dfs2(lis[i]);
		}
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			if ((tag[i] != tag[j]) && g[i][j]) {
                // 此处为缩点
            }
		}
	}
}

接下来我们来说说Tarjan算法，这个算法相对于上个算法理解起来要困难些.

在Tarjan算法中，最为重要的两个数组是 dfn[] 和 low[] ， dfn[i] 记录的是编号为i的节点在DFS的整个过程的顺序，它会在第一次访问到 $i$ 节点时更改，此后将不会变化；low[i] 表示的是 i 与其之后遍历到的节点所能到达的节点中 dfn 最小的 dfn ，在初始化时 dfn[i]=low[i] .

Tarjan算法在运行时会生成一棵搜索树，但是我们知道，图!=树，因为图中有一些边会使得“树”有环，自然，在生成树后，有一些边会直接指向已遍历的节点，没遍历的节点会在下一步当作自己的孩子进行遍历，而指向已遍历节点的边就是导致“树”有环的罪魁祸首.按照定义，当发现有这种边的存在时，需要更新当前节点的 low[] 值，需要更新为 min(dfn[这些边指向的节点]) .而理所当然地，我们也要被孩子节点更新 low 值为 min(low[孩子节点]) .

现在我们聚焦某一个点 $i$，观察 dfn[i] 与 low[i] 的关系，以下是两种情况：

dfn[i]>low[i] ，这说明 $i$ 或其子孙节点存在边连到 $i$ 上方的节点.
dfn[i]=low[i] ，这说明 $i$ 以及其子孙节点无法连到 $i$ 上方的节点，那么这个点 $i$ 就是一个强连通分量在这颗搜索树的根.

但是，$i$ 的子孙节点有可能会组成另一个强连通分量，这意味着 $i$ 的子树的节点不一定和 $i$ 处在同一个强连通分量内，我们需要栈来解决这个问题.

现在，我们用一张图看一下 dfn[] 与 low[] 的关系。

在这张图中，有 (3,4,5,6) ，7 ，8 ，1 ，2 这四个强连通块.

下图是Tarjan算法的运行过程.

因为SCC模板就是Tarjan算法，所以在这里不放代码.

二分图的最大匹配

何为二分图？二分图是一种特殊的无向图，它的顶点可以被分为两个互斥的独立集 $U$ 和 $V$ 的图，使得所有边都是连结一个 $U$ 中的点和一个 $V$ 中的点（如下图所示）.

何为匹配？一个图的匹配是这个图中一些边所形成的集合，满足任意集合中的两条边都没有公共顶点.

解决这个问题的算法之一是匈牙利算法.在了解这个算法之前，我们先要了解一下何为增广路（增广轨/交错轨）.

增广路：若 $P$ 是图 $G$ 中一条连通两个未匹配顶点的路径，并且已匹配和未匹配的边（也就是属匹配边集 $M$ 的边和不属 $M$ 的边）在 $P$ 上交替出现，则称 $P$ 为相对于 $M$ 的一条增广路径.

不难发现，如果我们把 $P$ 中原来属于 $M$ 边从 $M$ 中删除，把 $P$ 中原来不属于 $M$ 边加入到 $M$ 中，变化后得到的新的匹配 $M’$ 恰好比原匹配多一条边.

而匈牙利算法就是不断寻找增广路 $P$ ，通过取反操作得到更大的匹配 $M’$ 来代替 $M$ .

代码如模板所示.

割点

是无向连通图中一个顶点 $v$ , 如果删除它以及它关联的边后，得到的新图至少包含两个连通分量.

这里同样使用Tarjan算法.

思路和求SCC的Tarjan算法类似，这里直接给出结论：

一个顶点 $u$ 是割点，当且仅当满足条件 $1$ 或 $2$.

$u$ 为树根，且 $u$ 有两棵及以上的子树（这很好理解吧）.
$u$ 不为树根，且满足存在一条 $(u,v)$ 为树枝边使得 dfn[u] <= low[v] ，即 $u$ 有一个孩子无法到达 $u$ 以上的点.

代码如模板所示.

桥

是无向连通图中的一条边，如果删除它，得到的新图包含两个连通分量.

求桥和求割点差不多，可以直接从代码看出差别，而且判断条件的理解也和求割点差不多，此处不过多赘述.

双连通图

不含割点的无向连通图.

双连通分量

无向连通图的最大双连通子图.

点双连通分量

通过找割点获得的双连通分量（层层递进.jpg

边双连通分量（模板没打）

通过找桥获得的双连通分量.

心得体会

主要是图论之前有接触过，所以理解概念会比较快，同时在这一周我把之前一直没弄懂的Tarjan算法搞懂了.

现在的问题主要是建边的技巧以及破题的能力，像这种题（[SDOI2010]所驼门王的宝藏），这些建边的技巧想不到.

图论的常识有些遗忘了，例如Dijkstra跑最长路不能保证时间复杂度这类东西.

2023-05-21发表2024-01-09更新题解3 分钟读完 (大约473个字)

题解：对称二叉树

思路

因为这道题只要求最大的节点数量，所以我们只用枚举“根节点”的位置，然后判断是否对称，如果对称，统计这棵子树的节点数并记录 ans 。
cnt 与 main 函数过于简单故不在此处展开赘述，单独看看 same 函数——判断是否对称。我们一次需要两个位置来判断对称，而这两棵子树对称，当且仅当它们的儿子们全部对称，便可以从此处向下递归。递归的两边就是同时向内收 (ls[RootR],rs[RootL]) 或同时向外放 (ls[RootL],rs[RootR])，如果不这样的话遍历的两个位置本身就不对称。基于此，我们再来看实现。

实现

在代码实现方面，存树我们使用两个列表 ls 与 rs，这里开成了一个结构体，除此之外，我们还需要一个 id 用于存储树上节点的 value 。其余部分和思路部分所论述的一样。

代码


/*头文件及数组略*/

bool same(long long x, long long y) {
    if (x < 0 && y < 0) return true;     // 如果两边遍历到此处均为空，这棵树仍然对称
    if (x < 0 || y < 0) return false;    // 前面把都为空的情况return了，这里是只有一个点为空的情况
    if (t[x].id != t[y].id) return false;  // 值不匹配
    bool r = same(t[x].ls, t[y].rs)&&same(t[x].rs, t[y].ls);  // 递归检查子树是否符合要求
    return r;  // 略(?)
}

long long cnt(long long u) {  // 简单的节点统计
    if (u < 0) return 0;
    return cnt(t[u].ls)+cnt(t[u].rs)+1;
}

int main() {
    /* 输入略 */
    for (long long i = 1; i <= n; i++) {
        if (same(i, i)) {  // 如果以i为根的子树对称，统计节点并记录ans
            ans = max(ans, cnt(i));
        }
    }
    cout << ans;
    return 0;  // 结束
}

组合数

乘法逆元

Extend-GCD 拓展欧几里得法

快速幂法

乘法逆元优化组合数

动态规划的基本性质以及几个重要概念

几个性质

几个重要概念

简单例题

各种动态规划的形态

线性DP

最长公共子序列(LCS)

最长上升子序列(LIS)

背包问题

记忆化搜索

解题步骤

区间DP

分块部分

矩阵部分

学习内容

学习内容的模板（以及图论常用模板）

二分图最大匹配（König算法）

强连通分量（SCC）以及缩点

割点

桥

点双连通分量

dijkstra算法

SPFA算法

学习内容——各种定义

强连通/连通图

子图

连通分量

强连通分量（SCC）

二分图的最大匹配

割点

桥

双连通图

双连通分量

点双连通分量

边双连通分量 （模板没打）

心得体会

思路

实现

代码

链接

最新文章

归档

标签

`Extend-GCD` 拓展欧几里得法

边双连通分量（模板没打）