〇. 前置知识
四边形不等式(几何意义上)
对于任意一个凸四边形(如图1),四个顶点分别为 $A,B,C,D$ ,其对角线交于点 $O$ ,则有 $AD+BC>AB+CD$ 以及 $AD+BC>AC+BD$ .
证明:
$\because AO+BO>AB\text{ and }CO+DO>CD$ (三角形两边长之和大于第三边)
$\therefore (AO+DO)+(BO+CO)>AB+CD$ (联立两不等式)
$\therefore AD+BC>AB+CD$
(同理可得 $AD+BC>AC+BD$)
四边形不等式(DP意义上)
这边主要都是些定义,因此不会有什么 针对定义的证明 。
定义1
设 $w$ 是定义在整数集合上的二元函数,对于任意整数 $i \leq i’ \leq j \leq j’$ ,若有 $w(i,j)+w(i’,j’) \leq w(i,j’)+w(i’,j)$ ,则称 $w$ 满足四边形不等式.[^1]
什么叫做定义在“整数集合上的二元函数”?就是 $w$ 函数有两个参数,它的值和参数均为整数.
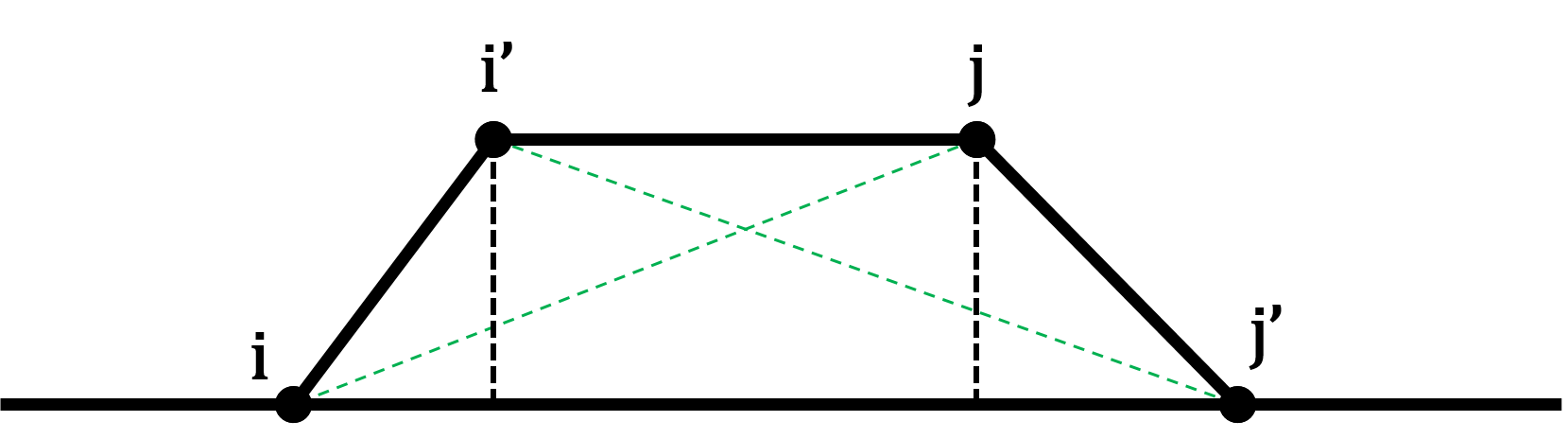
但是,这似乎跟四边形没有半点关系吧.我们不如形象一点,对于刚才的定义,我们将 $i,i’,j,j’$ 表示在一个不太严谨的数轴上,这个数轴上 $a,b$ 两点的距离是 $w(a,b)$,然后,将中间的两个点,也就是 $i’$ 和 $j$ 向上抬升一点(如图2),这个四边形(在 $i’=j$ 的情况下是三角形)就出来了.
定义2
这是 定义1 的特殊情况。
对于任意整数 $i < i+1 \leq j < j+1$ ,若有 $w(i,j)+w(i+1,j+1) \leq w(i,j+1)+w(i+1,j)$ ,则称 $w$ 满足四边形不等式.[^1]
没啥好说的。。。
单调性
设 $w$ 是定义在整数集合上的二元函数,对于任意整数 $i \leq i’ \leq j \leq j’$ ,若有 $w(i,j’) \geq w(i’,j)$ ,则称 $w$ 具有单调性.[^1]
一. 证明四边形不等式定理
四边形不等式定理
如果 $w(i,j)$ 满足四边形不等式和单调性,则使用动态规划计算 $f$ 数组的时间复杂度为 $\Theta(n^2)$ .
- 引理1
1
二. 引用
[^1]: 参考 罗勇军的博客——算法竞赛专题解析(10):DP优化(1)–四边形不等式
[^2]:F. Frances Yao原论文